Tick5 Tutorial 3

Home
Download
License
Screenshots
Manual
Tutorial
Development
Contact

3. It's a counting game

Now, our program can collect the status of the spots in the star pattern in Figure 2-1. The next step is to identify patterns these stones form, which basically is a counting game. For example, we start from the spot on the very top in the north, go all the way down to the south, and count like this: empty, empty, my stone, my stone, .... Bingo! It's a 5-in-a-row, we win! Or, like this: my stone, my stone, his stone... Oops, it's nothing!

The goal in this section is to implement a parser, so that the evaluator can use it to identify patterns in each of the four directions in Figure 2-1 , and then assigns a value to the move based on the patterns it forms. When being fed with a stream of stones and empties, the parser must be able to identify various patterns as shown in Figure 3-1.

Image of Threat Patterns

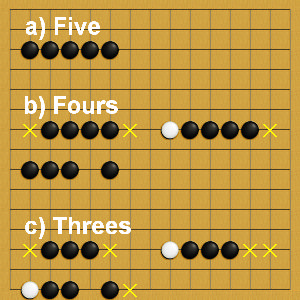
Figure 3-1

The yellow crosses in Figure 3-1 represent demanded empty spots. Figure 3-1a is a five which is a won pattern and is goal of the game. Figure 3-1b are respectively a straight four which is a winning pattern, a four and a broken four, which are threats that need immediate reaction. Figure 3-1c are respectively a straight three which is a threat that needs immediate reaction, a three and a broken three.

For completeness, our program also needs to identify two-stone (either consecutive or broken) and one-stone pattern, which have the potential to form a five-in-a-row. All these add up to nine patterns the parser must be able to identify.

Let's open boora-0.2.wz with a text editor and save it as boora-0.3.wz.

As we did in previous sections, we first define the interface of the parser class (Listing 3-1) and modify evaluator to test it (Listing 3-2.)

The parser class has one public member function parse(), which takes a stream of stones and empty spots as inputs. A parser instance can be created by calling newParser() with the color of stones in question. (see Listing 3-1)

------------------------------------------------
-- Parser class
------------------------------------------------
do
   -- parse a stream of stones and empties
   local function parse( parser, stream )
   end

   -- method table
   local methodtbl = { parse = parse }

   -- metatable
   local metatbl = { __index = methodtbl }

   -- creates an instance of parser class
   function newParser( color )
      local parser = { color = color }
      return setmetatable( parser, metatbl )
   end
end

                                           Listing 3-1

To get evaluate() ready, we create a parser instance, call its member function parse() with the stream of each direction, and print out those variables which count the numbers of the nine patterns identified. (see Listing 3-2)

   function evaluate( board, x, y, color )
      local parser = newParser( color )

      local x0, y0
      for dir, offset in pairs( _directions ) do
         print( dir )
         local stream, idx = {}, 1
         for i = -4, 4, 1 do
            x0 = x + i*offset.x
            y0 = y + i*offset.y

            if board:inboard( x0, y0 ) then
               stream[idx] = board:getstone( x0, y0 )
               idx = idx + 1 
            end
         end

         for j, stone in ipairs( stones ) do
            print( stone )
         end
         parser:parse( stream )
      end

      print( "fives: ",   parser.fives )
      print( "sfours: ",  parser.sfours )
      print( "fours: ",   parser.fours )
      print( "bfours: ",  parser.bfours )
      print( "sthrees: ", parser.sthrees )
      print( "threes: ",  parser.threes )
      print( "bthrees: ", parser.bthrees )
      print( "twos: ",    parser.twos )
      print( "ones: ",    parser.ones )
   end

                                             Listing 3-2

Play against the program, we see that counters are all nil. Let's add function initCounters() to initialize these counters. (Listing 3-3)

   -- initialize counters
   local function initCounters( parser )
      parser.fives = 0
      parser.sfours, parser.fours, parser.bfours = 0, 0, 0
      parser.sthrees, parser.threes, parser.bthrees = 0, 0, 0
      parser.twos = 0 
      parser.ones = 0 
   end

                                              Listing 3-3

Modify newParser(), accordingly.

   function newParser( color )
      local parser = { color = color }
      initCounters( parser )

      return setmetatable( parser, metatbl )
   end

                                           Listing 3-4

Play against the program, we see that all counters are zero. initCounters() takes effect.

Now we start to implement the counting game. However, the actual situations are much complex than the two examples as described at the beginning of this section. As a matter of fact, we are moving into the most complex part of this tutorial, implementing the parser. If you cannot completely understand the remaining contents, it doesn't matter, as long as you know that the parser identifies the nine patters, and the evaluator assigns a value to the move based on the identified patterns.

The parser is a Finite State Machine(FSM.) Figure 3-2 is its state transition diagram (STD).

Image of Parser FSM

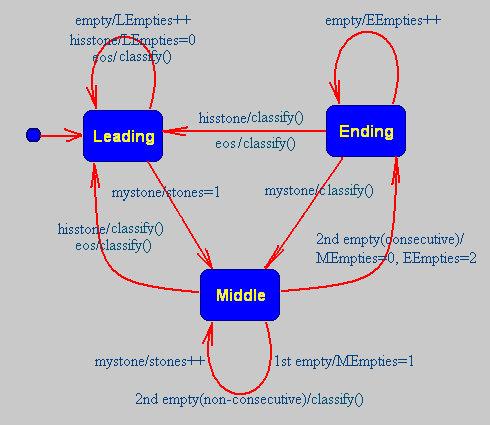
Figure 3-2

As can be seen, the FSM has three states (represented by rectangles): Leading, Middle and Ending. Leading is the state when the parser still hasn't encountered any stone of the color in question yet. It counts leading empty spots, but ignores the other player's stones. Middle is the state when the parser is counting stones of the color in question. Only one empty spot is allowed in the middle, which corresponds to either broken four or broken three. Ending is the state when the parser is counting ending empty spots.

There are four events that occur in the following occasions: 1) empty event occurs, when the parser encounters an empty spot; 2) mystone event occurs, when it encounters a stone of the color in question; 3) hisstone event occurs, when it encounters another player's stone; and 4) eos event occurs, when it reaches the end of the stream.

Those arrows represent transitions from one state to the other. For example, when eos event occurs and the parser is in "Ending" state, it invokes classify() to classify the pattern and transits to state "Middle," which is represented by the arrow point from "Ending" to "Leading" and labeled eos/classify().

Add function initFSM() which initializes variables related to the FSM. (Listing 3-5) They are respectively the state of the FSM, the number of stones in question (stones in the STD), leading empty spots (LEmpties in the STD), middle empty spots (MEmties in the STD), and ending empty spots (EEmpties in the STD).

   -- initialize Finite State Machine
   local function initFSM( parser )
      parser.state = "Leading"
      parser.stones = 0
      parser.leadingEmpties = 0
      parser.middleEmpties = 0 
      parser.endingEmpties = 0
   end

                                            Listing 3-5

Add function initStream()which initializes variables related to the stream. (Listing 3-6) They are respectively the stream and a pointer to the current position in the stream.

   -- initialize stream
   local function initStream( parser )
      parser.stream = nil
      parser.ptr = 0
   end

                                            Listing 3-6

Add function initParser()which calls all three initialization functions to initialize the parser class. (Listing 3-7)

   local function initParser( parser )
      initCounters( parser )
      initFSM( parser )
      initStream( parser )
   end

                                            Listing 3-7

Again, modify newParser()accordingly. (Listing 3-8)

   function newParser( color )
      local parser = { color = color }
      initParser( parser )
      return setmetatable( parser, metatbl )
   end

                                            Listing 3-8

We have done all necessary initialization to parser class. Let's go to parse() and implement the only public member function. (Listing 3-9) Basically, it's a while-loop that scans stream. It follows the STD in Figure 3-2 and invokes different handlers based on the status of the encountered spot. For example, if it encounters a stone of the color in question, it calls mystone(); if a empty spot, empty(). Upon reaching the end of the stream, it calls eos().

   local function parse( parser, stream )
      parser.stream = stream
      local stone = nil
      while next( parser ) do
         stone = parser.stream[parser.ptr]
         if stone == parser.color then
            mystone( parser )
         elseif stone == 0 then
            empty( parser )
         else
            hisstone( parser )
         end
      end

      eos( parser )
   end

                                            Listing 3-9

Function next() increases the pointer by one and returns true, if it hasn't reached the end of the stream; returns false, otherwise. (Listing 3-10)

   -- step to next spot
   local function next( parser )
      if parser.ptr >= table.getn( parser.stream ) then
         return false
      else
         parser.ptr = parser.ptr + 1
         return true
      end
   end

                                            Listing 3-10

Function mystone() is listed in Listing 3-11. It gets called when a stone of the color in question is encountered. As shown in the STD in Figure 3-2, if it is in "Leading" state, it sets counter stones to one and switchs to "Middle" state; if it is in "Middle" state, it increases stones by one; if it is in "Ending" state, it invokes classify() to determine the pattern, resets counters and switchs to "Middle" state.

   -- a stone of the color in question encountered
   local function mystone( parser )
      if parser.state == "Leading" then
         parser.stones = 1
         parser.state = "Middle"

      elseif parser.state == "Middle" then
         parser.stones = parser.stones + 1

      elseif parser.state == "Ending" then
         classify( parser )

         parser.stones = 1
         parser.leadingEmpties = parser.endingEmpties
         parser.middleEmpties, parser.endingEmpties = 0, 0
         parser.state = "Middle"

      else
         assert( false, "mystone(): unknown state "..parser.state )
      end
   end

                                            Listing 3-11

Similarly, we can implement empty() and hisstone(). Of them, empty() is more complex, and even more complex than emtpy() as shown in the STD in Figure 3-2. Please refer to the finished version of boora-0.3.wz for details.

Function classify()is called whenever a pattern can be identified. It first filters out pattern that does not have the potential to form a 5-in-a-row, then calls consecutive(), if there's no empty spot in the middle; broken(), if there's one. (Listing 3-12)

   -- is capable to form a 5-in-row or not
   local function capable( parser )
      return (parser.leadingEmpties + parser.stones + parser.middleEmpties + parser.endingEmpties ) >= 5 
   end

   -- classify pattern
   local function classify( parser )
      if not capable( parser ) then
         return
      elseif parser.middleEmpties == 0 then
         consecutive( parser )
      else
         broken( parser )
      end
   end

                                            Listing 3-12

Function consecutive() further identifies whether the pattern has empty spots at both ends or not, and then determines the pattern based on the number of stones encountered. (Listing 3-13)

   -- classify pattern that is consecutive
   local function consecutive( parser )
      if parser.leadingEmpties ~= 0 and parser.endingEmpties ~= 0 then
         if parser.stones == 1 then
            parser.ones = parser.ones + 1
         elseif parser.stones == 2 then
            parser.twos = parser.twos + 1
         elseif parser.stones == 3 then
            parser.sthrees = parser.sthrees + 1
         elseif parser.stones == 4 then
            parser.sfours = parser.sfours + 1
         elseif parser.stones >= 5 then
            parser.fives = parser.fives + 1
         end
      else
         if parser.stones == 1 then
            parser.ones = parser.ones + 1
         elseif parser.stones == 2 then
            parser.twos = parser.twos + 1
         elseif parser.stones == 3 then
            parser.threes = parser.threes + 1
         elseif parser.stones == 4 then
            parser.fours = parser.fours + 1
         elseif parser.stones >= 5 then
            parser.fives = parser.fives + 1
         end
      end
   end

                                            Listing 3-13

Function broken() doesn't care about empty spots at both ends, it just determines the pattern based on the number of stones encountered. (Listing 3-14)

   -- pattern that has an empty spot
   local function broken( parser )
      assert( parser.middleEmpties == 1 )

      if parser.stones == 1 then
         parser.ones = parser.ones + 1
      elseif parser.stones == 2 then
         parser.twos = parser.twos + 1
      elseif parser.stones == 3 then
         parser.bthrees = parser.bthrees + 1
      elseif parser.stones >= 4 then
         parser.bfours = parser.bfours + 1
      end
   end

                                          Listing 3-14

Play against the program. Make moves that form each of nine patterns, and check whether the parser can correctly identify them or not.

Now, the parser is up and running. It can tell us the patterns a move forms. We could explicitly use those counters to measure how good a move is. For example, if move can form a 5-in-a-row, it's the best; to compare two moves, we compare each of nine counters one by one. But for the sake of simplicity, we take another approach: assign a weight to each pattern, sum up the weighted counters of all nine patterns, and assign the scalar value to the move as its value. (Listing 3-15)

   function evaluate( board, x, y, color )
      local parser = newParser( color )

      local x0, y0
      for dir, offset in pairs( _directions ) do
         local stream, idx = {}, 1
         for i = -4, 4, 1 do
            x0 = x + i*offset.x
            y0 = y + i*offset.y

            if board:inboard( x0, y0 ) then
               stream[idx] = board:getstone( x0, y0 )
               idx = idx + 1 
            end
         end

         parser:parse( stream )
      end

      print( "fives: ", parser.fives )
      print( "sfours: ", parser.sfours )
      print( "fours: ", parser.fours )
      print( "bfours: ", parser.bfours )
      print( "sthrees: ", parser.sthrees )
      print( "threes: ", parser.threes )
      print( "bthrees: ", parser.bthrees )
      print( "twos: ", parser.twos )
      print( "ones: ", parser.ones )

      return ( parser.fives*5000 +
               parser.sfours*1600 + parser.fours*1400 + parser.bfours*1000 +
               parser.sthrees*160 + parser.threes*140 + parser.bthrees*100 +
               parser.twos*10 + parser.ones )
   end

                                                          Listing 3-15

Modify function makemove() of AI class to print out the value. (see Listing 3-16)

   -- a method that makes a move
   local function makemove( ai, board )
      local x, y, color = board:lastmove()
      if x ~= nil and y ~= nil then
         print( evaluate( board, x, y, color ) )
      end

      return randmove( board )
   end

                                          Listing 3-16

Play against the program. Make moves that form each of nine patterns, and make sure that the evaluator can correctly calculate their values.